Il nuovo logo e la Sezione Aurea

Siamo di Mercoledì, e come ogni mercoledì da ora in poi, posteremo un argomento che potrà riguardare qualsiasi tema ma guardandosi bene che il tutto abbia un collegamento con la musica o con il nostro Conservatorio.

Questo che vedete qui a fianco è il nuovo logo del nostro Conservatorio.
Se vedete un CD, da ora in poi, o una lettera o un gadget o qualsiasi cosa abbia quel disegnino impresso, allora riguarderà il Conservatorio "J.Tomadini" di Udine.

Logo che oltre a recare la scritta nominativa dell'Istituto, rappresenta il rigo musicale che impazzisce. Rigo in bianco su sfondo nero, ma sarà possibile anche trovare un rigo dorato o di qualche altro colore, sempre su sfondo nero o comunque scuro.

Fino a qui è chiara la questione, ma la cosa interessante è che il rigo non impazzisce a caso ma in base ad una rappresentazione della sezione aurea e di ciò che ne consegue.

E da qui parte il nostro argomento di oggi. Cos'è la sezione aurea? Da dove deriva? Perchè aurea? Cosa centra con la musica?...e così via.

---

La sezione aurea fu studiata dai Pitagorici i quali scoprirono che il lato del decagono regolare inscritto in una circonferenza di raggio r è la sezione aurea del raggio e costruirono anche il pentagono regolare intrecciato o stellato, o stella a 5 punte che i Pitagorici chiamarono pentagramma e considerarono simbolo dell'armonia.
A partire dal Rinascimento la Sectio Aurea acquista il crisma della bellezza estetica. Secondo Luca Pacioli ed Albrecht Durer, la SectioAurea o numero d'Oro, era l'elemento proporzionale analogico tra la figura umana e la natura oggettiva.
In botanica, fisica, zoologia, architettura, pittura e musica, oltre che in geometria in alcune relazioni riguardanti i poligoni regolari, la sezione aurea interviene in modo inesistente. Essa, che non è altro che un semplice rapporto di numeri, si incontra ovunque, in natura, come nella scienza e nell'arte, e "contribuisce alla bellezza di tutto ciò che circonda".
L'equilibrio armonico che si percepisce nelle opere dell'arte classica e rinascimentale è il risultato di un'impostazione che si realizza in alcuni principi compositivi come l'utilizzo della sezione aurea. In realtà vari esperimenti suggeriscono che la percezione umana mostra una naturale preferenza per le proporzioni in accordo con la sezione aurea.

Dal punto di vista matematico la sezione aurea (nota anche come rapporto aureo, numero aureo, costante di Fidia e proporzione divina), è indicata abitualmente con la lettera greca Φ (phi), corrisponde al numero:

Graficamente, la sezione aurea può essere rappresentata da un segmento diviso in due parti a e b, tali che il rapporto tra l'intero segmento a+b e la parte più lunga a sia uguale al rapporto tra la parte più lunga a e la parte più corta b:

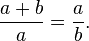
Anche le due parti a e b così ottenute sono tra loro in rapporto aureo, così come la parte più piccola con la differenza tra le due parti:

Dato un segmento di lunghezza 1, la sezione aurea può essere rappresentata algebricamente con la seguente proporzione:


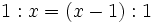
che, dopo alcuni passaggi, può essere riscritta come:



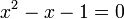
Questa equazione ha un'unica soluzione positiva:


Φ è un numero irrazionale, ed è l'unico numero reale per cui




La sezione aurea è legata alla sequenza di Fibonacci. Il rapporto tra due termini consecutivi {F_{n + 1}}, {F_n} di tale sequenza tende a Φ.

Φ è inoltre l'unità fondamentale del campo numerico algebrico ed è un numero di Pisot-Vijayaraghavan.
La sezione aurea ha interessanti proprietà se utilizzata come base di un sistema di numerazione.


RETTANGOLO AUREO


TRIANGOLO CON ANGOLI DI MISURA: 72°, 72°, 36°.
Dato un triangolo isoscele i cui angoli alla base misurano 72° ciascuno, e l’angolo al vertice misura 36°, la bisettrice di un angolo alla base divide il lato obliquo opposto nel punto d’intersezione in due segmenti in modo tale da creare una sezione aurea. Infatti il triangolo ABC è simile al triangolo BCD. E da questo risulta che:

AC:BC=BD:DC
e dunque:
AC:AD=AD:DC


TRIANGOLO CON ANGOLI DI MISURA: 36°, 36°, 108°.
Dato un triangolo isoscele i cui angoli alla base misurano 36° ciascuno, e l’angolo al vertice misura 108°, il lato obliquo e la differenza tra la base e il lato obliquo danno vita a una sezione aurea. Infatti il triangolo CDE è simile al triangolo ABD della figura precedente.


PENTAGONO E TRIANGOLI IN ESSO CONTENUTI
All’interno di un pentagono, ogni lato forma con due diagonali (il segmento che unisce due punti non adiacenti) un triangolo dagli angoli con misura 72°, 72°, 36°, con le proprietà spiegate in precedenza. Ogni lato forma, con il punto d’incontro di due diagonali consecutive, un triangolo dagli angoli 36°, 36°, 108°, con le proprietà descritte in precedenza. Cioè il lato del pentagono regolare è la sezione aurea di una sua diagonale e il punto d' intersezione tra due diagonali divide ciascuna di esse in due segmenti che stanno nel rapporto aureo.


SPIRALE AUREA

Se all’interno di un rettangolo aureo si disegna un quadrato con lato uguale al lato minore del rettangolo, il rettangolo differenza sarà anch’esso un rettangolo aureo. Si ripeta l’operazione per almeno cinque volte al fine di avere un effetto visivo adeguato. Si punti la punta del compasso sul vertice del quadrato che giace sul lato lungo del rettangolo e si tracci l’arco che unisce i gli estremi dei due lati che formano l'angolo scelto. Si ripete l'operazione per ogni quadrato disegnato in modo da creare una linea continua.

AVVICINANDOSI ALLA MUSICA
Euclide, primo a trattare in modo esplicito di S.A. C'invita a risolvere il seguente problema:

«Dividere una retta data in modo che il rettangolo compreso da tutta la retta e da una delle parti sia uguale al quadrato della parte rimanente».

Proposizione elegante ed affascinate, ma che per il suo aspetto prettamente geometrico potrebbe forse risultare di non semplice — o comunque non d'immediata comprensione — a tutti coloro che non hanno fatto, contemporaneamente alla musica, anche della matematica e della geometria il proprio pane quotidiano.

Ma il nostro Euclide — un po' più avanti nel suo trattato — esporrà poi la famosa «definizione IIIa», la cui formula d'apertura, per i molti secoli a venire, verrà adottata da tutti gli studiosi come la più autentica espressione del concetto di S.A.

«Si dice che una retta risulta divisa in estrema e media ragione, quando tutta quanta la retta sta alla parte maggiore di essa come la parte maggiore sta a quella minore».

A toglierci dall'imbarazzo della “definizione” sarà il matematico italiano Leonardo Fibonacci (Leonardo Pisano) che, dopo aver “navigato” in lungo e in largo nella cultura arabo-matematica, nel 1202 ci consegnerà il suo famoso trattato intitolato Liber Abbaci. Lì, fra le altre migliaia di cose riportate, in un breve capitoletto e tramite un simpatico quanto efficace “quesito” (“proposizione” se volete) sulla prolificità dei conigli, il Fibonacci esporrà, senza peraltro rivelarci espressamente alcunché, una “magica” quanto antica serie numerica che solo in tempi più recenti prenderà poi il suo nome.

Questi i primi tredici termini della futura e denominata «Serie di Fibonacci», che compaiono nel Liber Abbaci (Fibonacci 1857:284) in relazione a quell'ipotetico e “curioso” numero progressivo di coppie di conigli procreate nel corso di un anno (Quot paria...):

1.2.3.5.8.13.21.34.55.89.144.233.377.16

Questa serie matematica ricorrente possiede numerose ed interessanti proprietà. Citeremo: 1) la più evidente, cioè che ogni numero è la somma dei due precedenti; 2) la più straordinaria (al caso nostro), ossia che tre numeri consecutivi estrapolati in un punto qualsiasi della successione (fatta eccezione per i primissimi termini) sono, grazie ad una straordinaria approssimazione, eccellenti valori numerici per la realizzazione di segmenti in proporzione aurea.

Ora, se dal punto di vista pratico l'applicazione di proporzioni auree nelle arti visive (pittura e architettura ad esempio) può essere facilmente intuito (ovvero una suddivisione più o meno elaborata dello spazio in porzioni auree) in campo musicale — causa non indifferente il fattore «tempo» — la faccenda risulta assai più complessa.

Per fare un primo semplice esempio, immaginiamo l'ascolto di un brano musicale composto da 144 battute in 4/4, e che all'attacco della mis. 90 sia contraddistinto da un evento timbrico, dinamico o formale di notevole rilievo, o comunque tale, da farci percepire nettamente la transizione dal primo segmento di 89 btt. al successivo di 55. In teoria, in fase di ascolto, dovrebbe aver luogo una percezione auditiva delle due sezioni del brano in proporzione aurea; a patto però, che la scansione metronomica del «tempo musicale» sia sufficientemente regolare, metronomicamente costante cioè, così da garantire una corrispondenza fra lo scorrere del «tempo cronometrico» e il numero di battute del brano. Sarebbe infatti sufficiente una diminuzione agogica a metà dell'esecuzione, per rendere nullo l'effetto di S.A. fra i due “segmenti”; le cui proporzioni, nel caso della nostra elementare esemplificazione, dipendono esclusivamente dalla sequenza e durata numerico-temporale delle battute.

---

Par maggiori informazioni andate qui:
http://www.sectioaurea.com/sectioaurea/S.A.&Musica.htm
http://it.wikipedia.org/wiki/Sezione_aurea
http://www.liceoberchet.it/ricerche/sezioneaurea/presentaz.htm